En classe

Un peu d’histoire
L’histoire de la trigonométrie semble avoir débuté il y a environ 4 000 ans. Nous savons de façon certaine que les Babyloniens déterminaient des approximations de mesures d’angles ou de longueurs de côtés de triangles rectangles. Plusieurs tables de nombres gravés sur de l’argile séchée en témoignent.

Les applications de la trigonométrie sont nombreuses et très variées. Les applications mentionnées sont souvent des utilisations pratiques, notamment en navigation, pour l’orientation, pour la construction d’édifices…
Elle est aussi souvent employée dans des matières insoupçonnées comme en théorie de la musique, en psychologie…
Un métier : Le géomètre-topographe
À l’aide d’appareils spécialisés (théodolite, tachéomètre…), le ou la géomètre-topographe relève des mesures permettant de représenter, sur un plan ou sur une carte, les formes et les détails (naturels ou artificiels) d’un terrain, en n’omettant aucun détail : niveaux d’altitude, arbres, poteaux télégraphiques, murs…
Ces relevés lui permettent d’établir des plans et des cartes d’implantation d’ouvrages sur ordinateur, en utilisant des logiciels de métré ou de DAO (dessin assisté par ordinateur), des SIG (systèmes d’information géographique), des images satellites, …

A/ Mission 1 : Activité : Le triangle rectangle


Rappel : La somme des angles d’un triangle est égale à 180°.
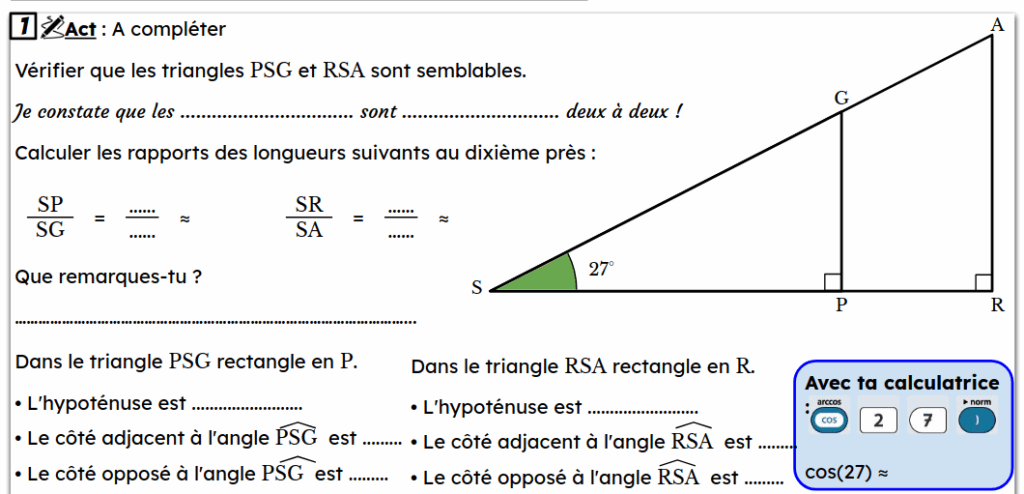
B/ Mission 3 : Je découvre le cosinus

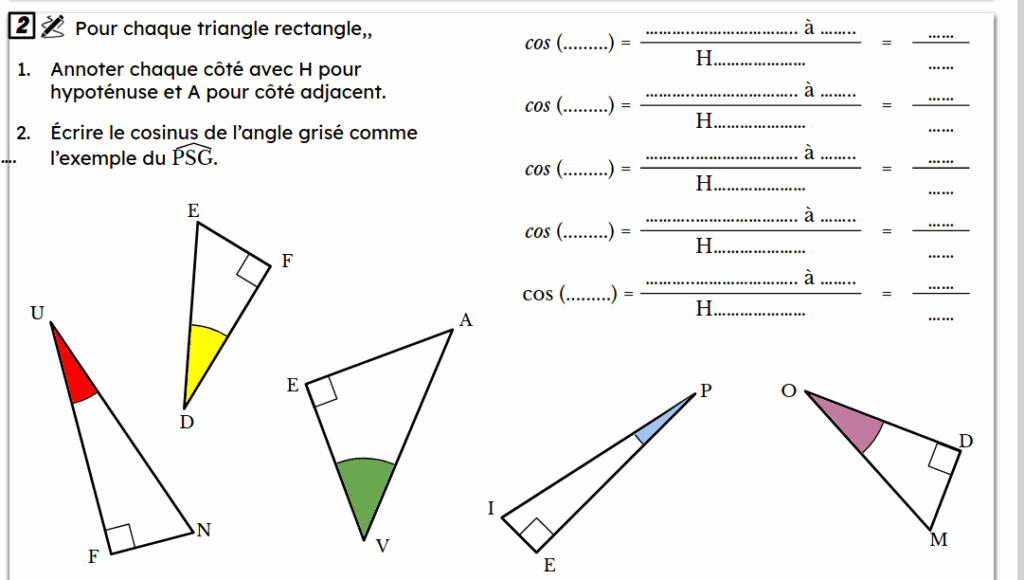
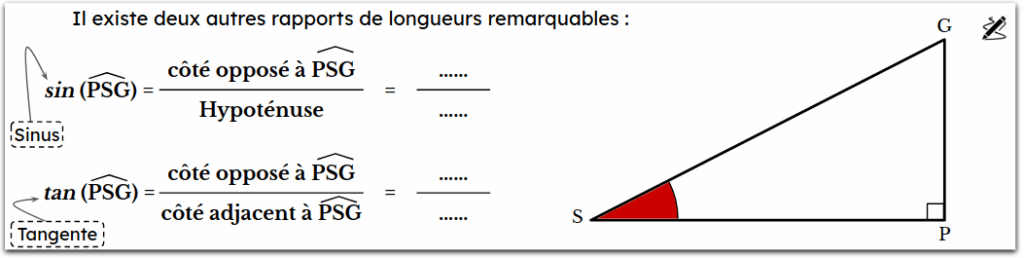
C/ Mission 4 : Le sinus et la tangente
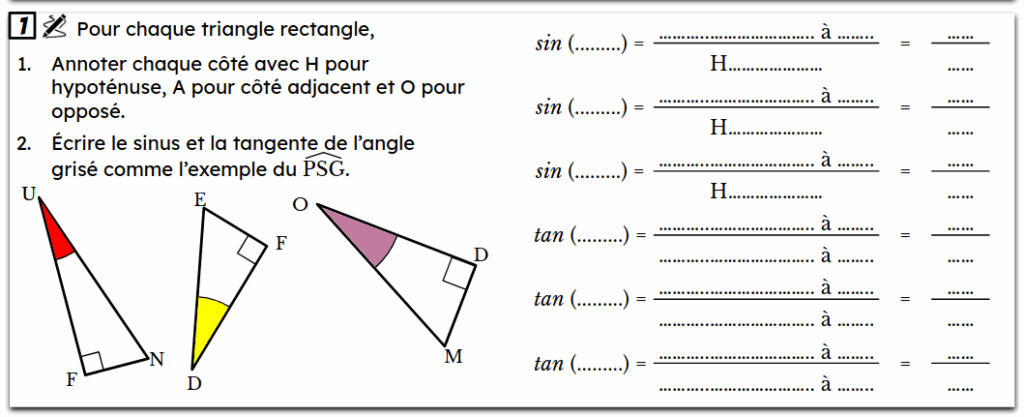

D/ Mission 5 : Utilisation de la calculatrice
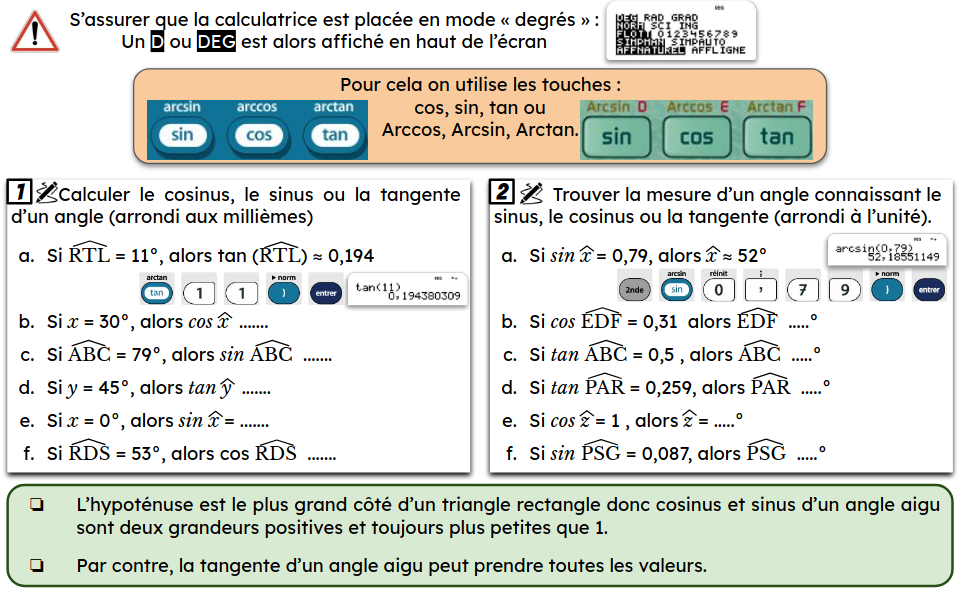

E/ Mission 6 : Calculer le mesure d’un angle
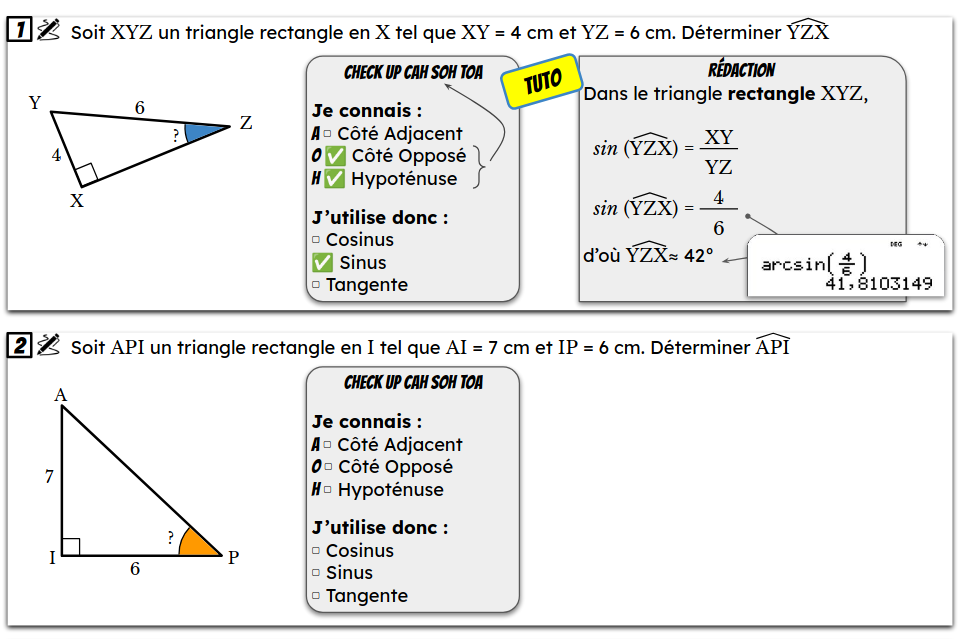
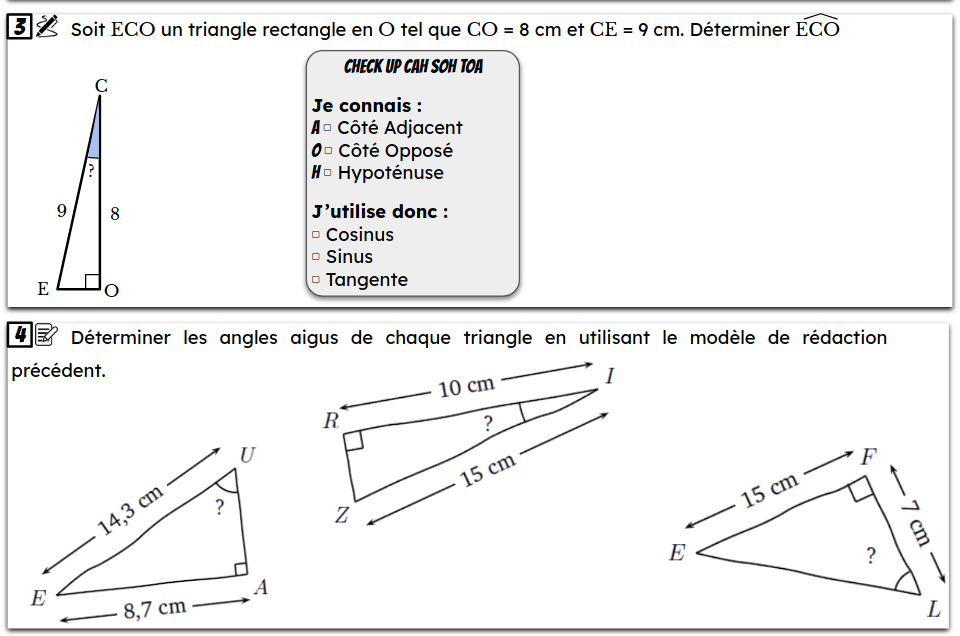
F/ Mission 7 : Calculer la longueur d’un côté
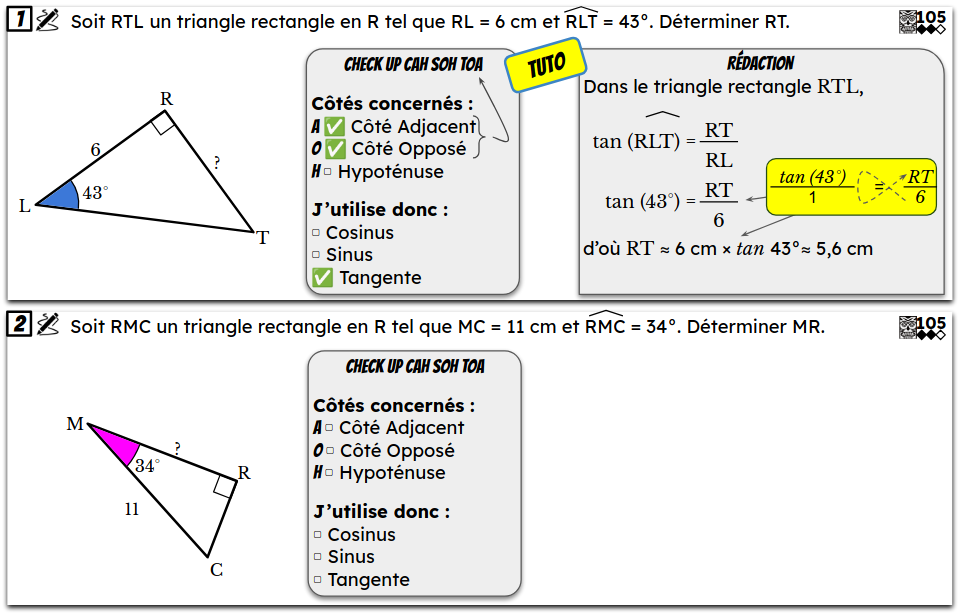
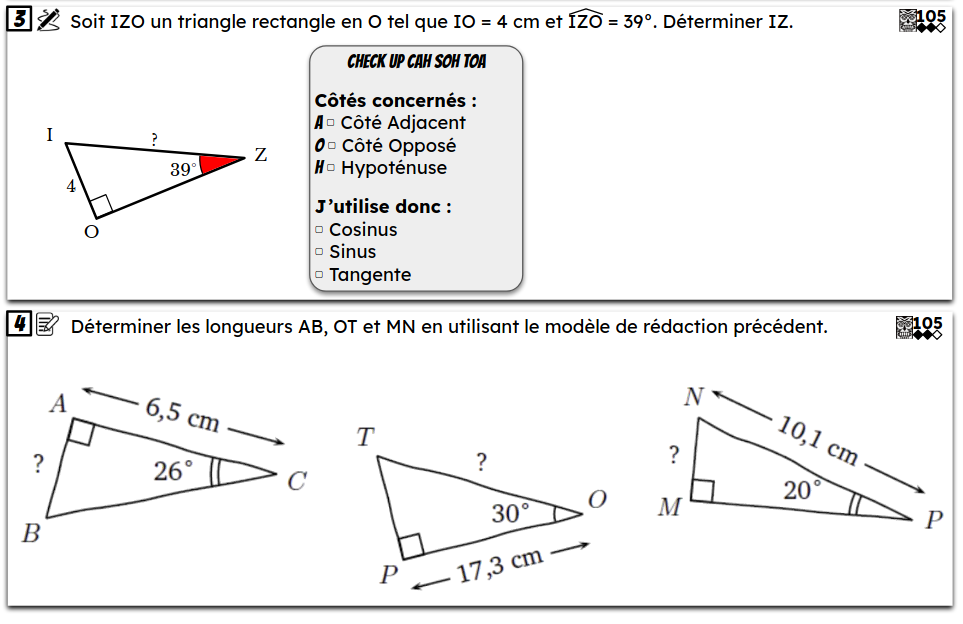
Maths Numériques

A/ Résoudre un problème : Calculer la hauteur d’un immeuble
Pour mesurer la hauteur BH d’un immeuble, un géomètre procède ainsi : il se place à 5 m de l’immeuble et mesure l’angle IOHˆ ; il trouve 76,8∘. Le point O représente l’œil de l’observateur : OP=1,70 m.
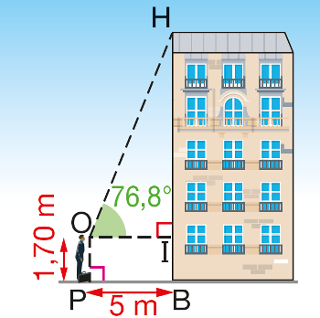
- Calculer la longueur HI en m. Donner une valeur approchée au cm près.
- Calculer alors une valeur approchée de la hauteur du bâtiment.

B/ Calculer les angles : Dans le Triangle (3,4,5)
MRT est le triangle rectangle représenté ci-dessous.
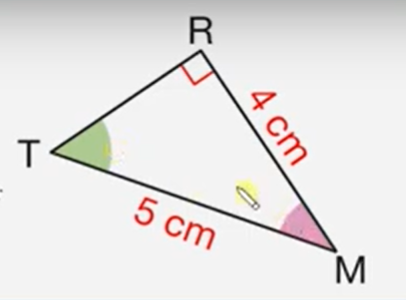
1. Déterminer la mesure de l’angle RMT. Donner une valeur approchée à l’unité près.
2. Utiliser la somme des mesures des angles d’un triangle pour déterminer une valeur approchée de la mesure de RTM.
Correction :

Reconnaître le côté adjacent et le côté opposé
Sinus, cosinus et tangente ?
Calculer la longueur
Calculer la mesure d’un angle