Activité :
- Trace deux triangles quelconques assez grands.
- Mesure ses angles.
- Additionne ses mesures.
- Que constates tu ?

Cours

A/ Somme des mesures des angles dans un triangle
Propriété :
Dans un triangle, la somme des mesures des trois angles est égale à 180°.
Démonstration :
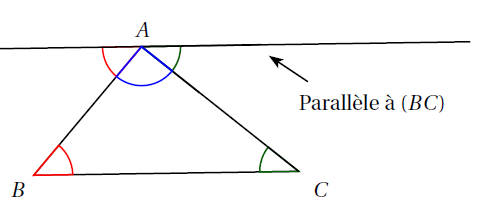
On trace la parallèle à la droite (BC) passant par A.
Les angles rouges sont alternes-internes ainsi que les angles verts.
Ainsi, les angles rouges et les angles verts ont la même mesure.
On en déduit que dans le triangle ABC :
B/ Application à un triangle quelconque
A toi de jouer :
Calculer l’angle .
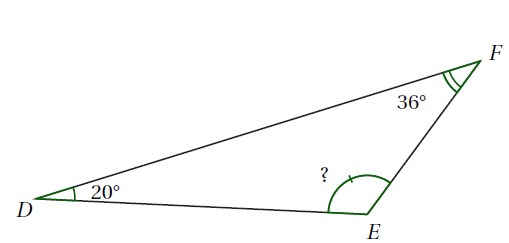
Solution :
Dans un triangle, la somme des mesures des angles est égale à 180° donc
C/ Cas d’un triangle isocèle
Propriété :
Un triangle isocèle a les deux angles de sa base égaux.
Premier cas :
Deuxième cas :
Même triangle isocèle mais avec 50° comme avec de bases.
D/ Cas du triangle équilatéral
Propriété :
Si un triangle est équilatéral alors chacun de ses angles mesure 60°.
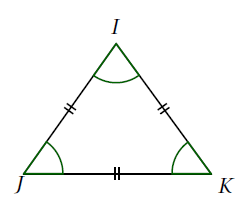
Démonstration
Le triangle est équilatéral donc ses 3 angles ont la même mesure.
donc
Ainsi
Exercice maths numériques
Mission 1
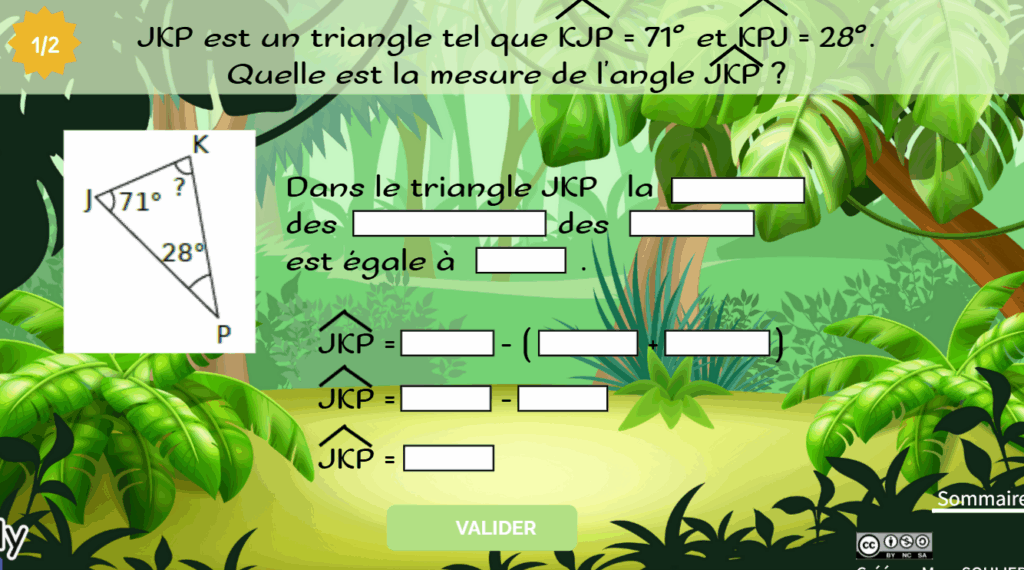
MIssion 2

Indice Mission 1
La sommes des mesures des angles est égales à 180°
180° – 99 ° = 81°
Réponse mission 2
Les exercices
A/ Fiche : Utiliser la somme des angles d’un triangle
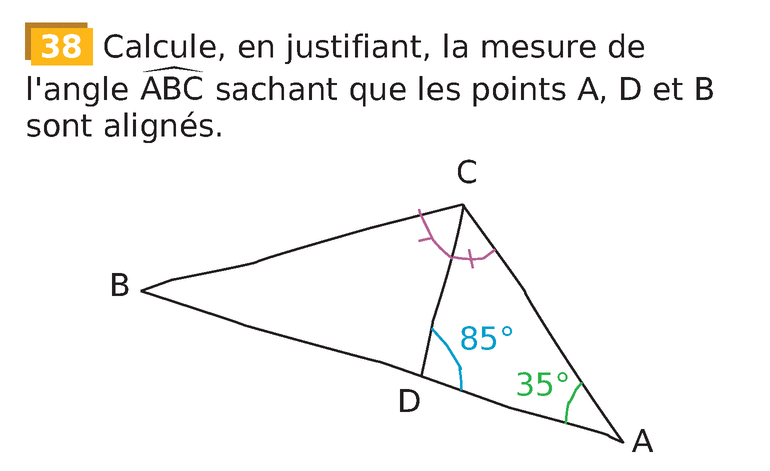
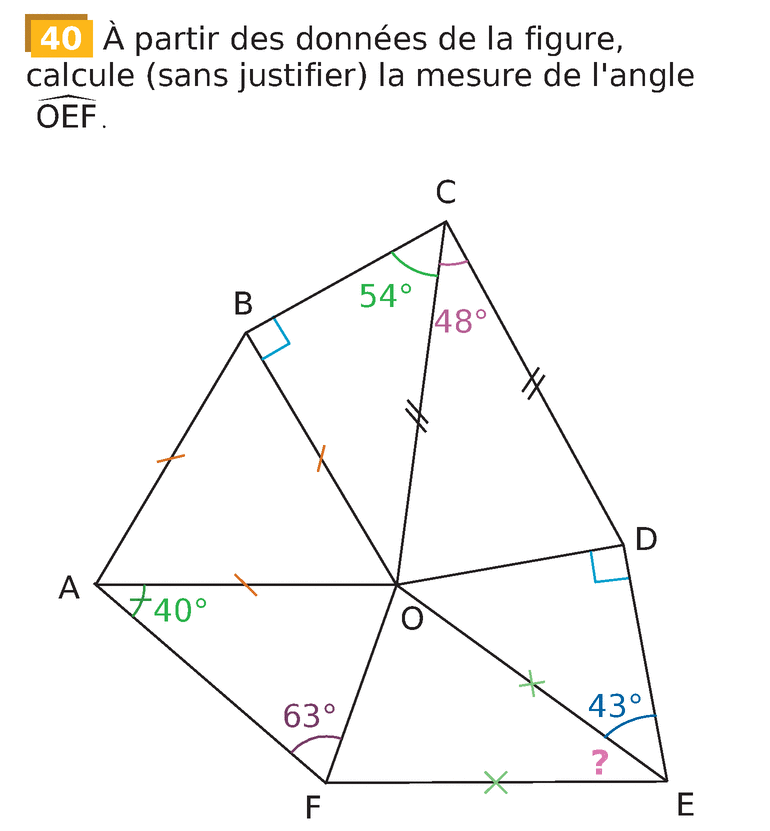
B/ Problèmes
Page 239 du Livre Sésamath – Cycle 4

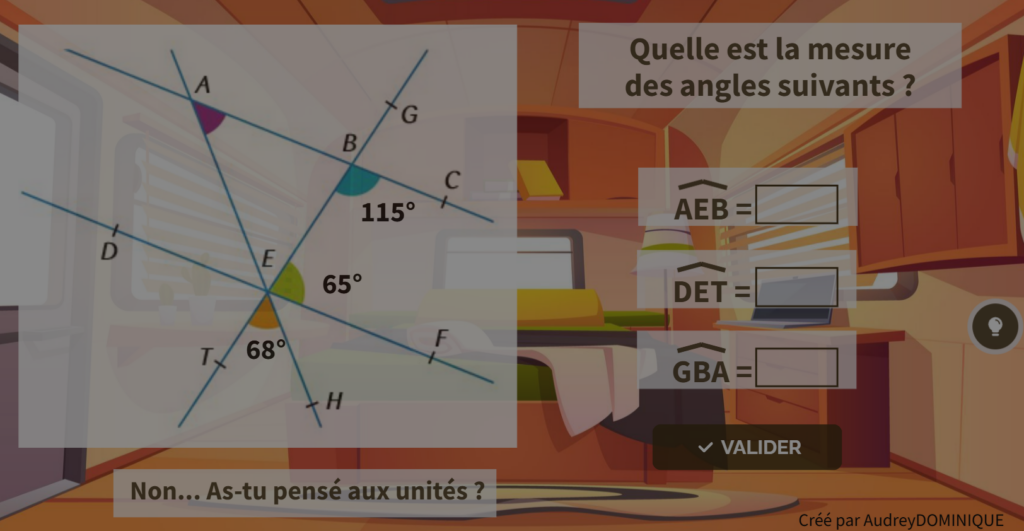
Maths Numériques


J’apprends à programmer avec Scratch

