En classe

Compétences travaillées
- Utiliser l’inégalité triangulaire pour savoir si je peux construire un triangle
Reconnaitre le cas particulier où les points sont alignés - Construire des triangles dont on connaît les longueurs des 3 côtés
- Résoudre un problème de périmètre
Ecrire un calcul avec plusieurs opérations une seule ligne
A/ Mission 1 : Construire un triangle connaissant 3 longueurs.
Ex 4 p 234 du livre
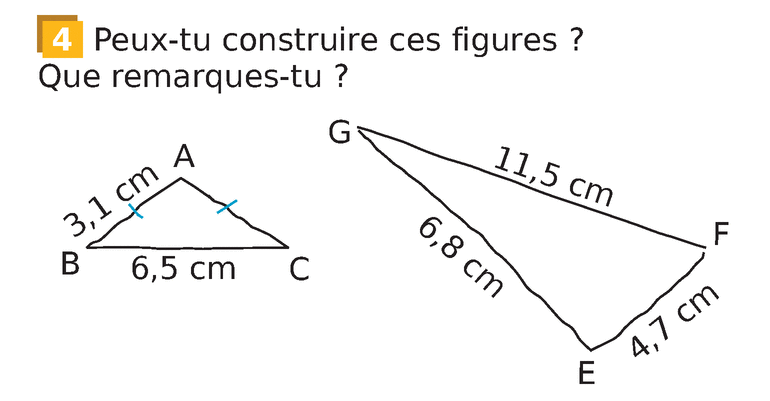
B/ Mission 2 : Comprendre l’inégalité triangulaire
Propriété : Dans un triangle, la somme des longueurs de deux côtés est supérieure à la longueur du troisième côté.
Exemple : Dans un triangle ABC, on a
AC + CB > AB
AB + BC > AC
BA + AC > BC
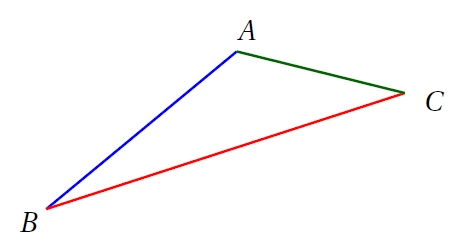
Remarque :
Des inégalités sont évidentes car BC > AB et BC >AC.
Conséquence :
Cela signifie que pour pouvoir construire un triangle dont on donne les longueurs des trois côtés, il suffit de vérifier que la somme des deux plus petites longueurs est supérieure à la troisième.
Exemple 1 :
Peut-on construire un triangle ABC tel que AB=8 cm, AC=4 cm et BC =2 cm ?
Correction :
.
.
.
.
Exemple 2 :
Peut-on construire un triangle IJH tel que IJ=7,2 cm, IH=4,5 cm et HJ=3,3 cm ?
Correction :
.
.
.
.
Méthode en vidéo :
C/ Mission 3 : Et si les points sont alignés…
Propriété :
Si A, B, C sont trois points tels que AB+BC=AC
Alors le point B appartient au segment [AC].
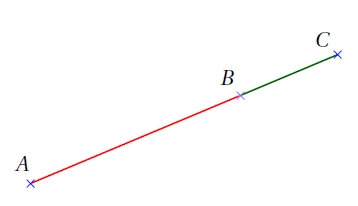
Remarque : Le cas réciproque est évident.
Si un point B appartient à un segment [AC] alors AB+BC=AC.
D/ Mission 4 : Et en rap, ça donne quoi ?
Exercices du livre

Livre p 234
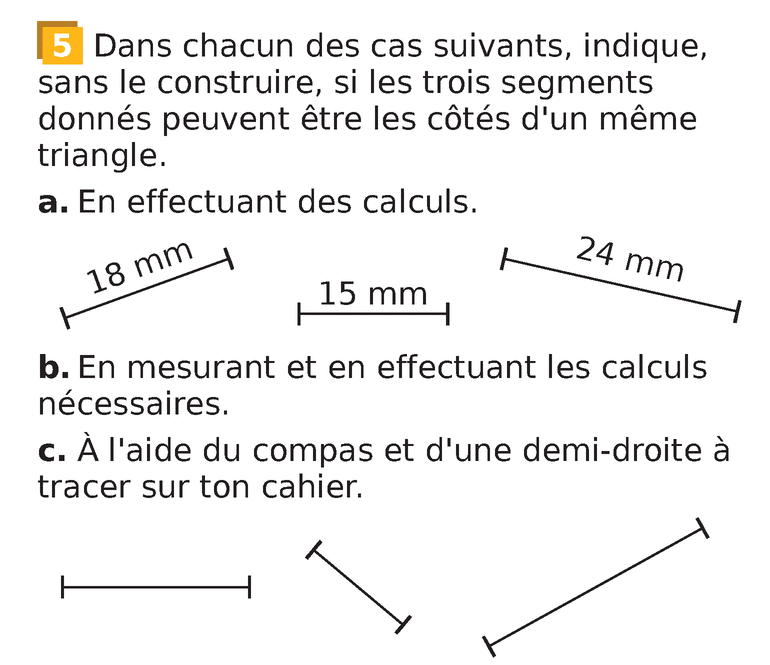
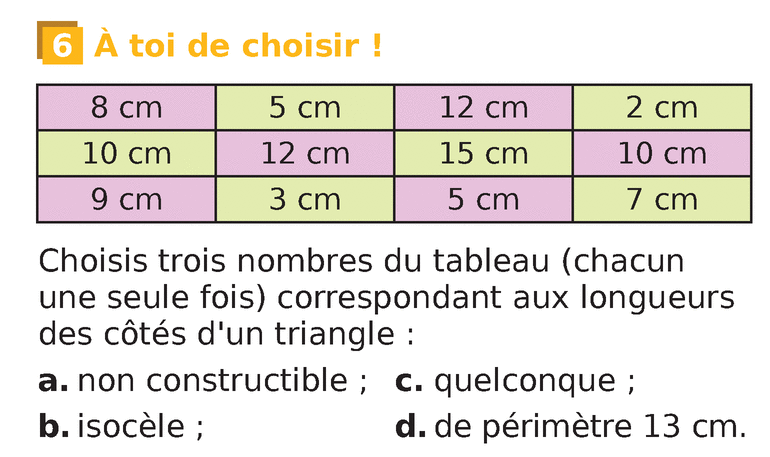

Livre p 235




Maths Numériques

Exercices :
Inégalité triangulaire
Utiliser l’inégalité triangulaire
Énigmes :
Énigme sur les triangles
Triangles isocèles



