En Classe

Compétences travaillées
- Comprendre la notation
- Utiliser une échelle
- Calculer une échelle
- Résoudre un problème
Tout le cours en vidéo
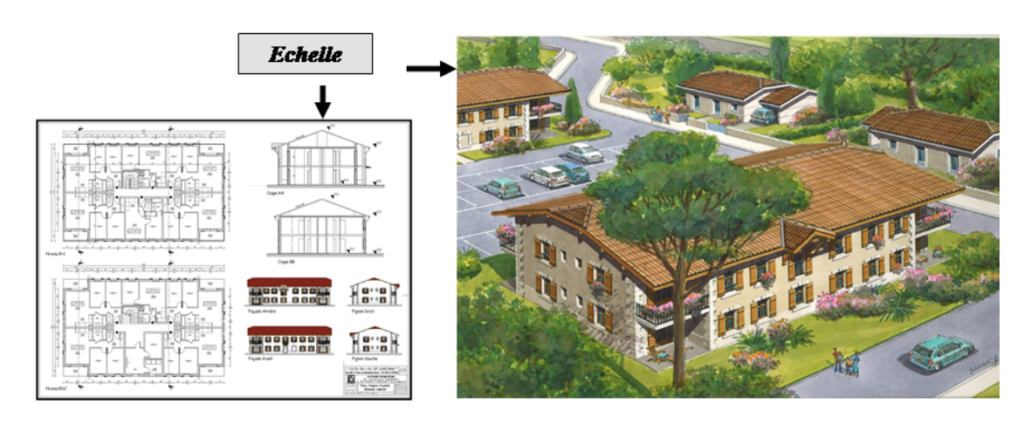
A/ Définition d’une échelle
Définition :
L’échelle d’un plan est le coefficient de proportionnalité entre les distances sur le plan et les distances réelles, exprimées dans la même unité:
B/ Utiliser une échelle
Explication en vidéo
Exemple :
Sur une carte à l’échelle ,
1 cm sur la carte représente 200 000 cm dans la réalité,
c’est à dire 2 000 m donc 2 km.
| Distance sur la carte en cm | 1 | 8 | 16 | 3,8 |
| Distance dans la réalité en km | 2 |
Remarque :
On utilise un tableau de proportionnalité.
Attention :
Il faut bien préciser les unités de longueurs à chaque étape.
A toi de jouer :
A quelle distance réelle correspond une longueur mesurée de 8,3 cm sur une carte à l’échelle ?
Correction :
C/ Calculer une échelle
Explication en vidéo :
Exemple :
Sur un plan, un appartement est représenté par un carré de côté 10 cm. La longueur réelle du côté du carré est de 9 m. Calculer l’échelle de ce plan.
Résolution :
L’échelle s’écrit sous la forme d’une fraction.
On cherche donc son numérateur et son dénominateur.
On divise la distance du plan par la distance réelle, exprimée dans la même unité :
Ainsi, l’échelle de ce plan est égale à .
Attention :
Le numérateur est le dénominateur de la fraction doivent être exprimé dans la même unité.
A toi de jouer :
Le modèle réduit d’un bateau de 25 m mesure 10 cm.
Quelle est l’échelle de réduction ?
Correction :
D/ Agrandissement – Réduction
Définition :
- Si l’échelle est supérieure à 1, il s’agit d’un agrandissement.
- Si l’échelle est inférieure à 1, il s’agit d’une réduction.
• Exemple 1
Le négatif d’une photographie est un rectangle de 24 mm sur 36 mm. La photographie est un agrandissement du négatif, sa longueur est 16,2 cm.
1/ Calculer l’échelle
2/ Calculer la largeur de la photographie.
Solution :
1/ Je convertis dans la même unité : 16,2 cm = 162 mm.
Méthode : Pour calculer une échelle, mettre le 1 de référence dans le tableau de proportionnalité au niveau des longueurs les plus petites.

donc x = ( 162 × 1 )  36 = 4,5.
36 = 4,5.
donc 4,5 mm sur la photo représentent 1 mm sur le négatif.
Ainsi, l’échelle de ce plan est égale à > 1,
il s’agit donc bien d’un agrandissement.
2/ La largeur du négatif est égale à 24 mm,
donc la largeur de la photographie est 24 × 4,5 = 108 mm = 10,8 cm
• Exemple 2
Un monument de longueur 110 m est représenté par une maquette de longueur 44 cm. Calculer l’échelle.
Solution :
Je convertis dans la même unité, ici les cm : 110 m = 11 000 cm.

donc x = ( 110 000 × 1 )  44 = 250 .
44 = 250 .
donc 1 cm sur la maquette représente 250 m en réalité.
L’échelle est x < 1, il s’agit bien d’une réduction.
Fiches :

Exercices

A/ Comprendre la notation
Ex 25 p 139

B/ Utiliser une échelle
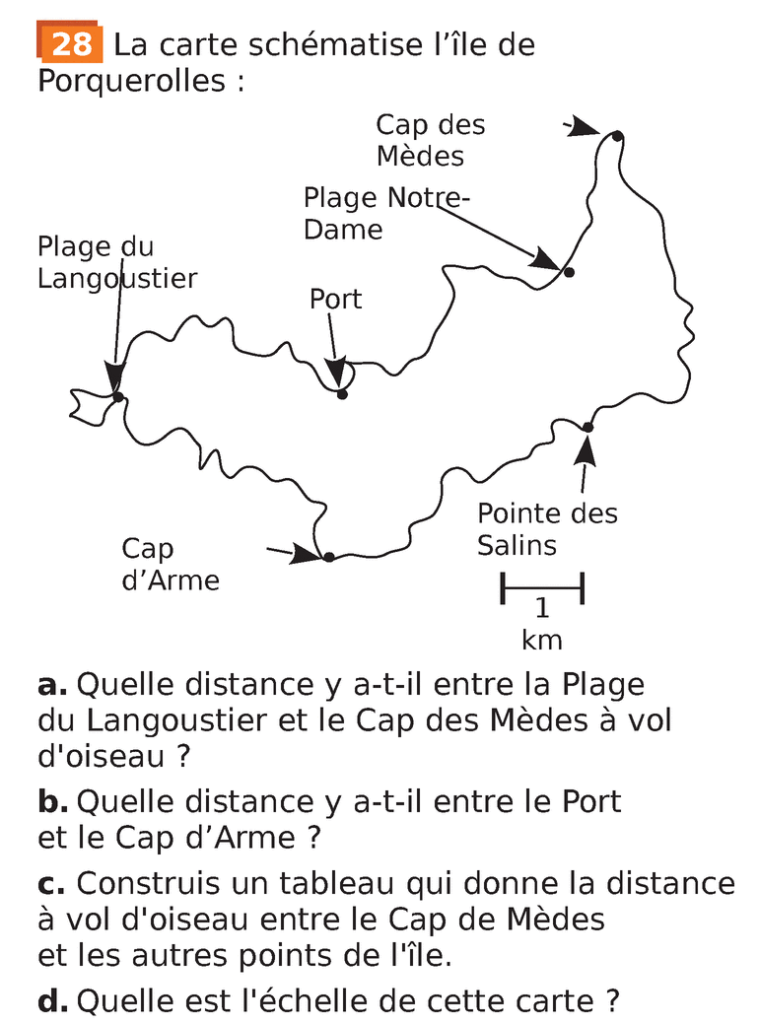
Ex 28 page 139
C/ Calculer une échelle
Ex 26 page 139

D/ Résoudre un problème
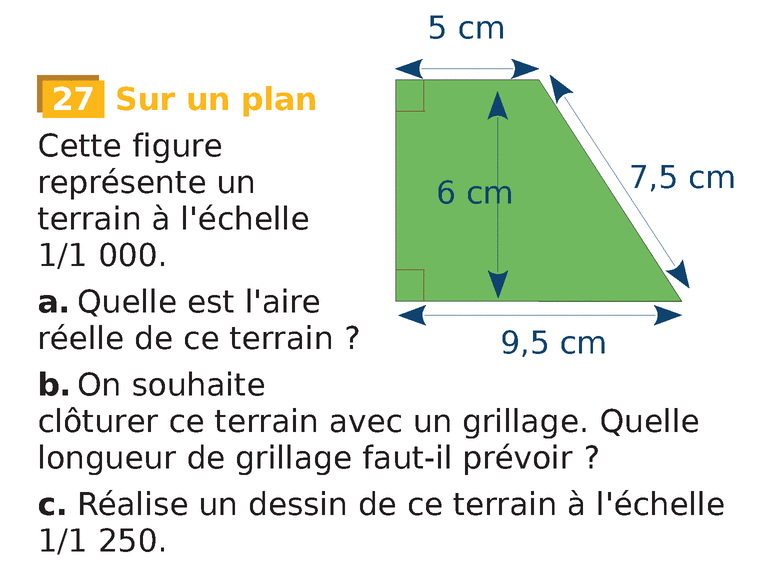
Ex 27 page 139
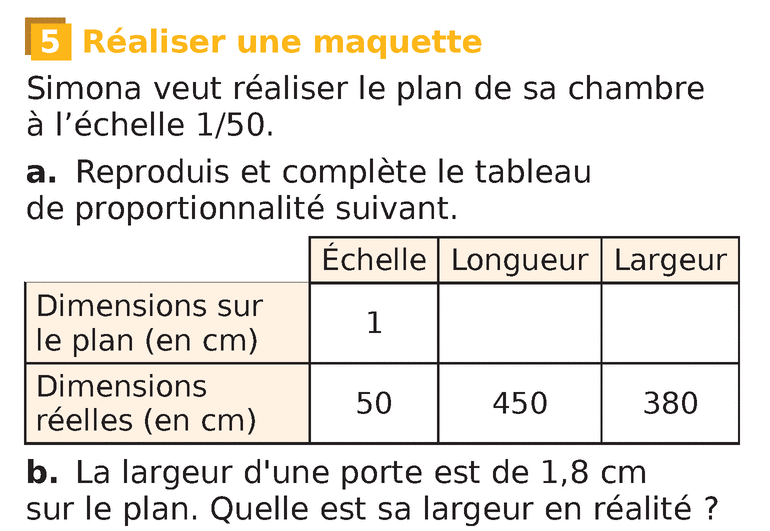
Ex 5 page 140
E/ Questions flash
Maths Numériques


