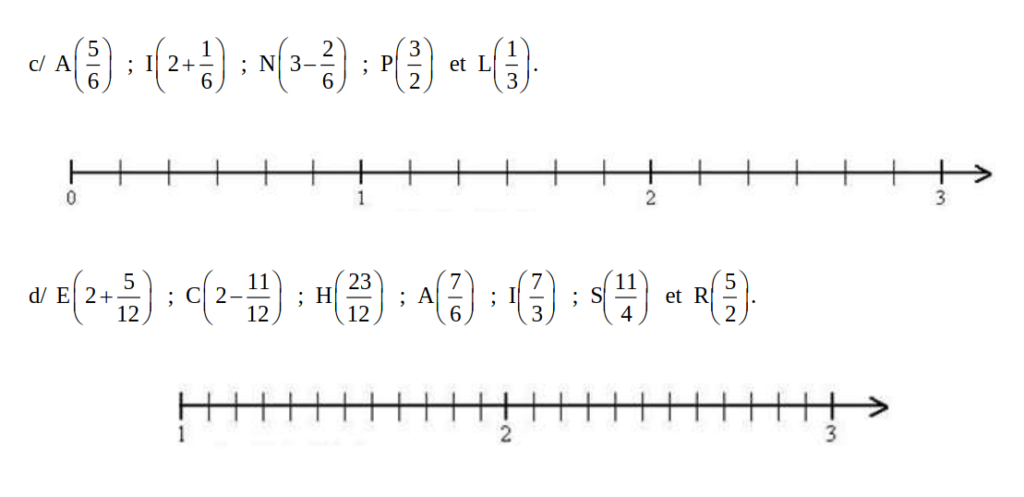En classe

Compétences travaillées
- Donner l’écriture décimale d’un quotient quand c’est possible.
- Placer une fraction sur une demi-droite graduée.
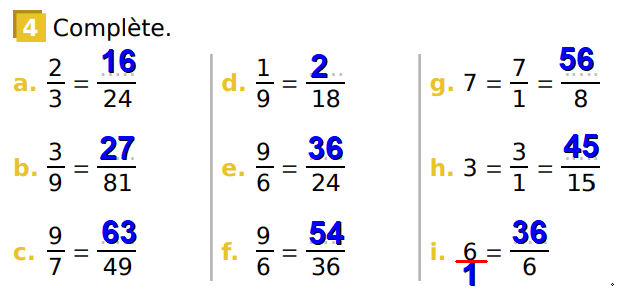
- Compléter des égalités.
- Déterminer si deux quotients sont égaux ou non.
- Simplifier une fraction.
- Résoudre des problèmes de proportion.
Activités : deux problèmes de proportion
Problème 5 p 50

Indice : faire un shéma pour représenter la situation.
Problème 9 p 50

A/ Ecriture fractionnaire d’un quotient
Définition :
Soient a et b deux nombres avec b≠0.
Le quotient de a par b est le nombre qui, multiplié par b, donne a.
On le note en écriture fractionnaire :
Exemple 1 :
Compléter l’égalité ci-dessous :
A toi de jouer :
Ex 1 page 44

Exemple 2 :
- Le quotient peut s’écrire sous forme d’un nombre décimal.
Exemple 3 :
- Le quotient ne s’écrit pas sous forme d’un nombre décimal.
- On donne ici une valeur approchée au millième près.
A toi de jouer :
Ex 5 p 44

Indice : Utilise ta calculatrice.
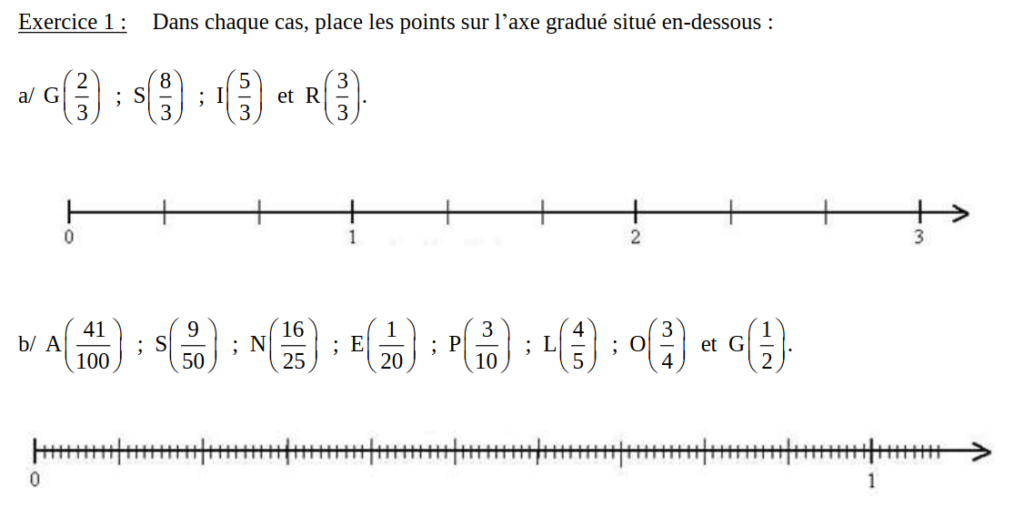
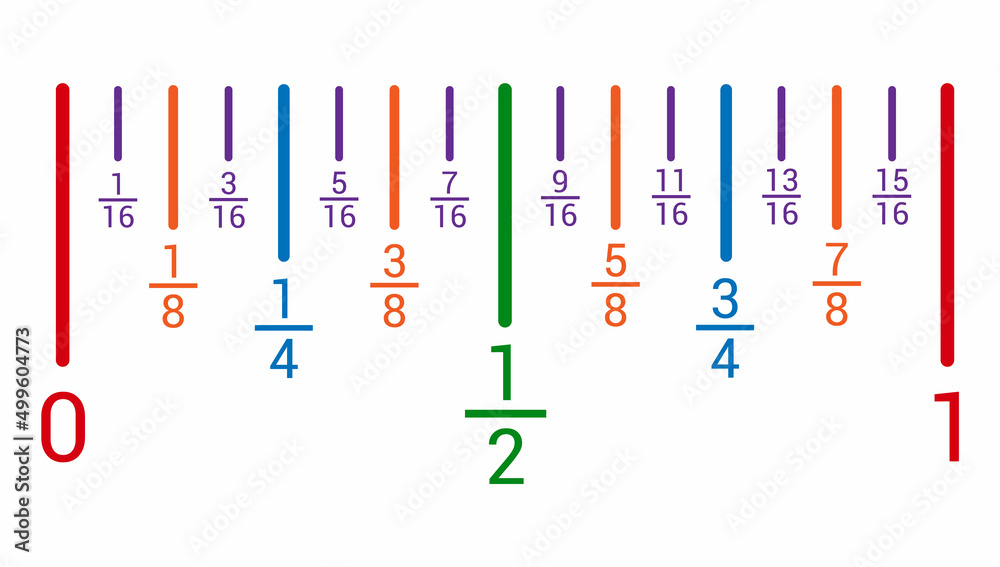
B/ Placer une fraction sur une demi-droite graduée
Exemple :
Pour placer sur la demi-droite graduée ci-dessous,les fractions et , il faut couper l’unité en 3 parties égales.
Comme l’unité est partagée en 6, on regroupe les graduations par 2.

Placer les fractions sur la droite graduée :
C/ Fractions égales
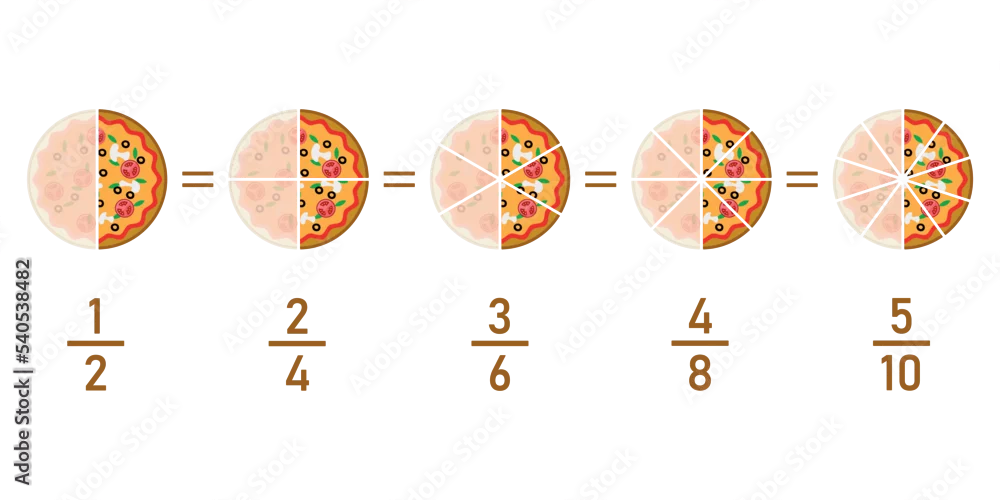
Règle des fractions égales :
Un quotient ne change pas si on multiplie (ou divise) son numérateur et son dénominateur par un même nombre non nul.
On obtient une fraction égale : c’est le même nombre mais avec une écriture différente.
Exemple 1 :
- On multiplie le numérateur et le dénominateur par 10.
Exemple 2 :
- On divise le numérateur et le dénominateur par 3.
A toi de jouer :
Ex 7 page 44
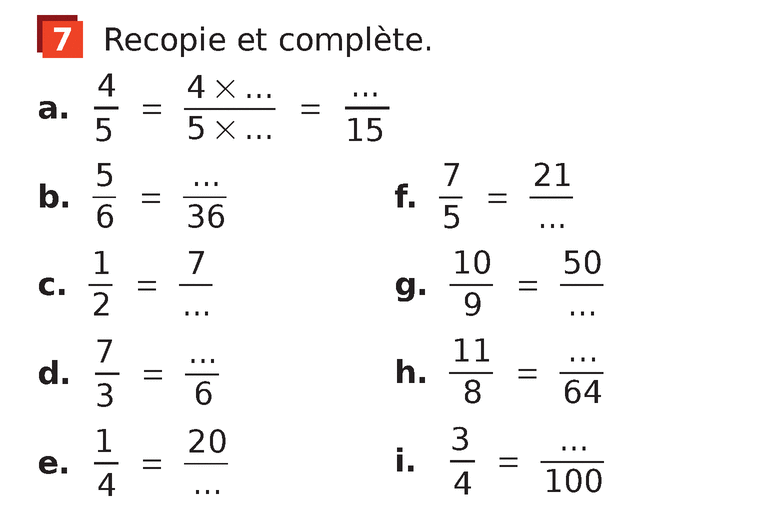
D/ Simplifier une fraction
Principe : Simplifier une fraction, c’est écrire une fraction qui lui est égale mais avec un numérateur et un dénominateur plus petits.
Exemple 1 :
On divise le numérateur et le dénominateur par 2.
Exemple 2 :
On divise le numérateur et le dénominateur par 5.
Méthode :
On cherche un diviseur commun au numérateur et au dénominateur.
On s’arrête quand il n’y a plus de diviseur commun.
On dit que la fraction est irréductible.
Aide : Revoir les critères de divisibilité.
A toi de jouer Niveau 1 :
Simplifie la fractionA toi de jouer Niveau 2 :
Simplifie les fractions suivantes :Exercices

A/ Comprendre l’écriture fractionnaire
Ex 2 page 44

Ex 3 page 44
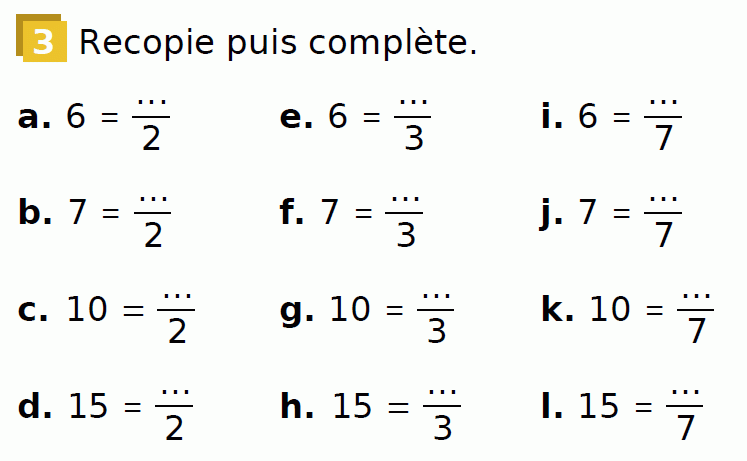
Ex 4 page 44

Ex 6 page 44
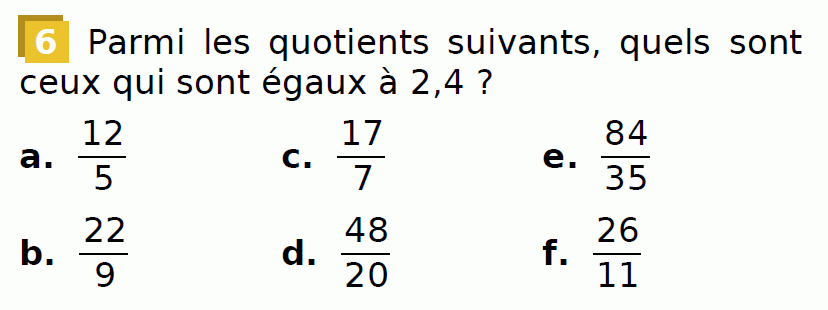
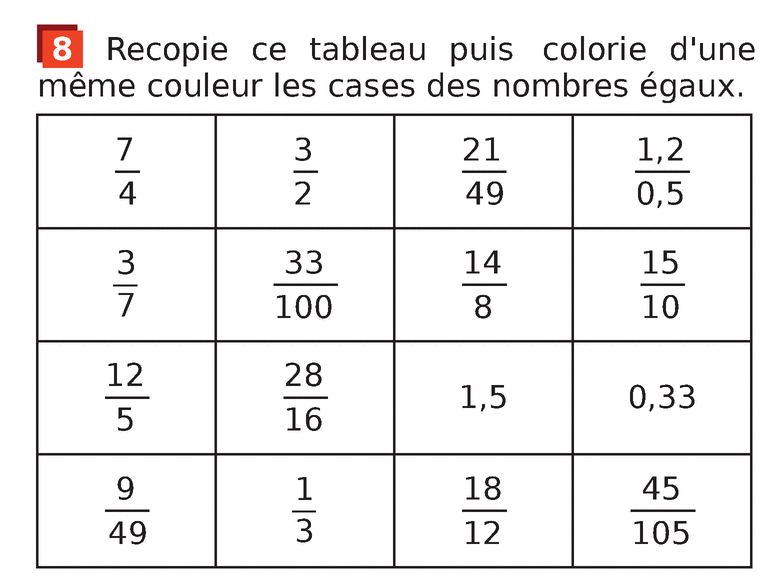
C/ Fractions égales
Ex 8 page 44
D/ Simplification de fraction
Ex 14 page 45

Aide : Revoir les critères de divisibilité.
Ex 15 page 45

Ex 16 page 45
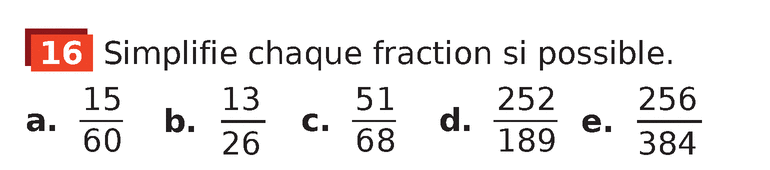
Ex 17 page 45

Ex 18 page 45

E/ Résoudre un problème
Problème 1 page 50

Fiches d’exercices:
Droite graduée
Fractions égales
Simplifier des fractions
( Cahier sesamath 5ème )

Questions flash
Correction de quelques exercices
Maths Numériques


Jaicompris.com : Exercices corrigés en vidéo
Exercice 1
« Pouvez-vous me donner une fraction plus simple égale à
Exercice 2


Simplifications guidées de fractions
Quotients égaux
Simplifications de fractions