Cours

A/ La règle des signes qui se suivent
Règle :
On peut simplifier les écritures en supprimant les parenthèses et les signes « + » sans changer la valeur de l’expression.
Exemples :
A = ( +2 ) + ( +4 ) = 2 + 4 = 6
B = ( –3 ) + ( –5 ) = – 3 – 5 = –8
C = ( +5 ) + ( –2 ) = 5 – 2 = 3
D = ( +3 ) + ( –3 ) = 3 – 3 = 0
Remarque :
Cette règle ne permet pas de simplifier deux signes « – » qui se suivent.
Méthode :
Pour simplifier une écriture, on peut appliquer la règle des signes suivante :
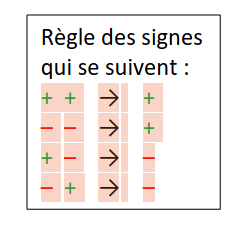
A toi de jouer :
Ex 36 page 26

Remarque :
Il n’est pas juste d’appliquer la règle des signes qui se suivent pour le calcul de 4 – ( –7 + 9 ) … Ici, il faut d’abord respecter la priorité des parenthèses.
Preuve :
4 – ( –7 + 9 ) = 4 + 7 + 9 = 20
ce qui est faux
car
4 – ( –7 + 9 ) = 4 – ( +2 ) = 4 – 2 = 2
B/ Suppression des parenthèses
Méthode :
Règle :
Cas n°1 :
Si la parenthèse est précédée d’un signe « + »,
il n’y a pas de problème. On supprime la parenthèse et on conserve les signes de chacun des nombres.
Cas n°2 :
Si la parenthèse est précédée d’un signe « – « ,
comme « Soustraire un nombre revient à ajouter son opposé »,
il faut donc dans ce cas, prendre l’opposé de l’expression de l’ensemble de la parenthèse, c’est à dire « changer » le signe de chacun des termes entre les parenthèses. On dit que l’on distribue le signe « – « .
Rappel :
S’il n’y pas de signe, cela signifie que le nombre est positif.
Exemples :
Effectuer les calculs suivants de deux manières différentes.
A = 3 – ( 1 – 5 )
A =
A =
A = 3 – ( 1 – 5 )
A =
A =
B = 4 + ( –7 + 9 )
B =
B =
B = 4 + ( –7 + 9 )
B =
B =
A toi de jouer :
Effectuer les calculs suivants de deux manières différentes.
C = (–3) – ( –6 + 8 )
D = ( –3 + 11 ) + ( –7 + 2 )

